삽입 정렬(Insertion Sort)
-배열을 정렬된 부분(앞부분)과 정렬 안 된 부분(뒷부분)으로 나누고, 뒷부분의 가장 왼쪽 원소를 앞부분의 적절한 위치에 삽입하여 정렬되도록 하는 과정을 반복
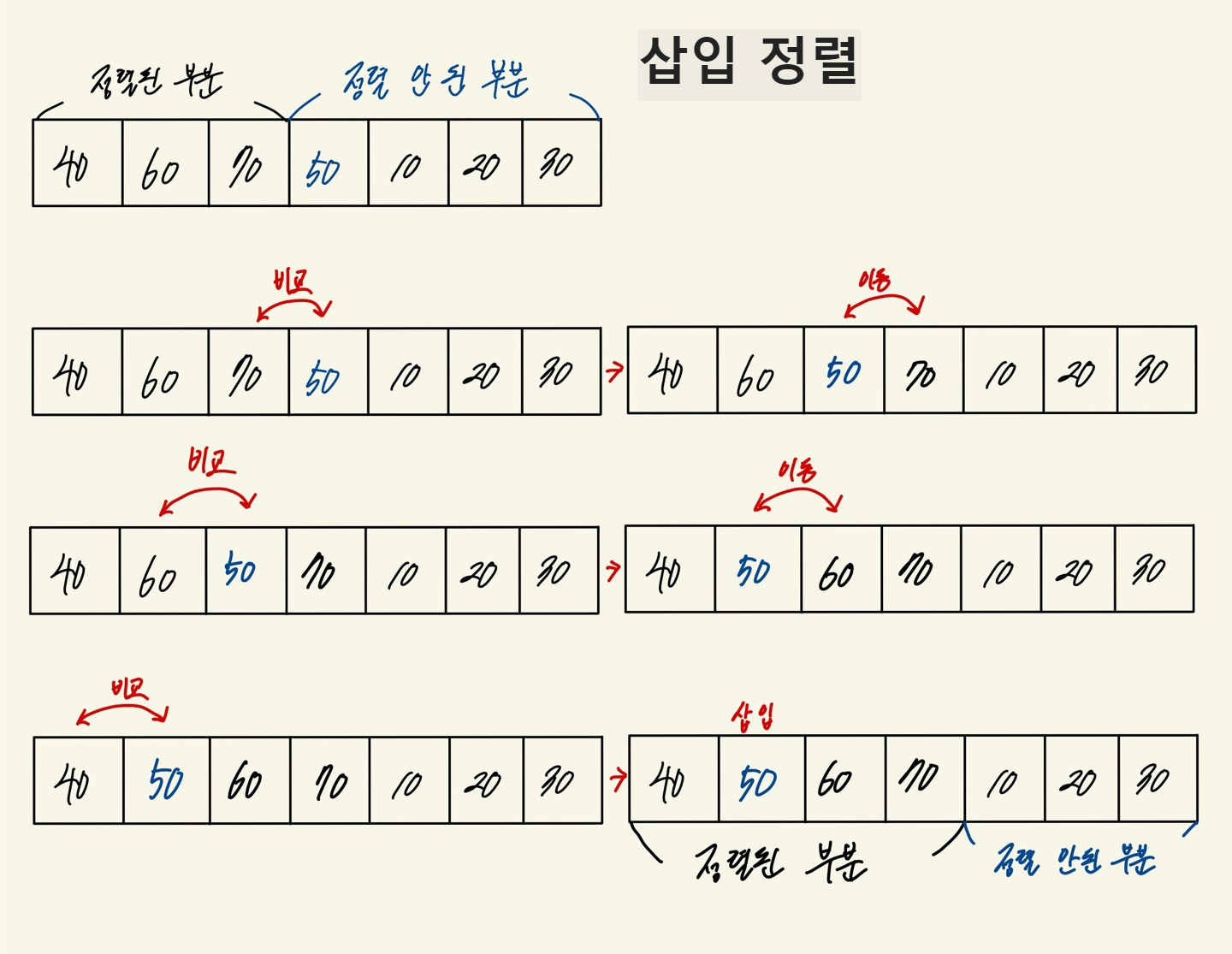
-정렬된 부분의 원소 수가 1개 늘어나고, 동시에 정렬이 안 된 부분의 원소 수는 1개 줄어듦
-반복하면, 뒷부분에는 아무 원소도 남지 않고, 입력이 정렬됨
알고리즘
입력: 크기가 n인 배열 A
출력: 정렬된 배열 A
for i=1 to n-1
CurrentElement = A[i]
j <- i-1
while(j>=0) and (A[j] > CurrentElement)
A[j+1]=A[j]
A[j+1] <- CurrentElement
return A
시간 복잡도
1. 최악 경우
for루프가 (n-1)회 수행
-i=1일 때 whilie루프 1회 수행
-i=2일 때 최대 2회 수행
...
-마지막으로 최대 (n-1)회 수행
루프 내부의 line5~6이 수행되는 총 횟수
=>1+2+3+...+(n-2)+(n-1)=n(n-1)/2
루프 내부는 O(1)
>> n(n-1)/2*O(1)=O(n^2)
2. 최선 경우
입력이 이미 정렬되어 있는 경우
-항상 각각 CurrentElement가 자신의 왼쪽 원소와 비교 자리 이동 x >> 원래 자리에 위치
-while 루프의 조건도 항상 False => 원소의 이동 x
>>(n-1)번의 비교만에 정렬 종료
>> O(n)
3. 평균 경우
CurrentElement가 자신의 자리 포함 앞부분의 각 원소에 자리 잡을 확률이 같다고 가정
>> O(n^2/4) = O(n^2)
특징
-거의 정렬된 입력에 대해서 다른 정렬 알고리즘보다 빠름
ex) 입력이 앞부분은 정렬되어 있고 뒷부분(전체 입력의 20% 이하)에 새 테이터가 있는 경우
-입력의 크기가 작을 때 매우 좋은 성능
-퀵, 합병 정렬에서 입력 크기 작아지면 순환 호출 중단, 삽입 정렬을 사용
-Tim sort에서 입력 크기가 64이하 >> 삽입 정렬 호출
'알고리즘' 카테고리의 다른 글
| [알고리즘] 정렬 알고리즘 - 쉘 정렬 (5) | 2023.12.06 |
|---|---|
| [알고리즘]정렬 알고리즘 - 선택 정렬 (2) | 2023.11.30 |
| [알고리즘]정렬 알고리즘 - 버블정렬 (1) | 2023.11.29 |
